Link State Routing
Link state routing adalah teknik di mana setiap router berbagi pengetahuan tentang lingkungannya dengan setiap router lain di internetwork.
Tiga kunci untuk memahami algoritma Link State Routing:
- Pengetahuan tentang lingkungan sekitar: Daripada mengirimkan tabel routingnya, router hanya mengirimkan informasi tentang lingkungannya saja. Sebuah router menyiarkan identitasnya dan biaya link yang terhubung langsung ke router lain.
- Flooding: Setiap router mengirimkan informasi ke setiap router lain di internetwork kecuali tetangganya. Proses ini dikenal sebagai Banjir. Setiap router yang menerima paket mengirimkan salinannya ke semua tetangganya. Akhirnya, setiap router menerima salinan informasi yang sama.
- Berbagi informasi: Sebuah router mengirimkan informasi ke setiap router lainnya hanya ketika terjadi perubahan informasi.
Router Link State memiliki dua fase:
Banjir yang Dapat Diandalkan
- Keadaan awal: Setiap node mengetahui biaya node tetangganya.
- Keadaan akhir: Setiap node mengetahui keseluruhan grafik.
Perhitungan Rute
Setiap node menggunakan algoritma Dijkstra pada grafik untuk menghitung rute optimal ke semua node.
- Algoritma routing Link state disebut juga dengan algoritma Dijkstra yang digunakan untuk mencari jalur terpendek dari satu node ke setiap node lainnya dalam jaringan.
- Algoritme Dijkstra bersifat iteratif, dan memiliki properti bahwa setelah k iterasi algoritma, jalur dengan biaya terkecil diketahui untuk k node tujuan.
Mari kita jelaskan beberapa notasi:
- c( i , j): Biaya tautan dari node i ke node j. Jika node i dan j tidak terhubung langsung, maka c(i , j) = ∞.
- D(v): Mendefinisikan biaya jalur dari kode sumber ke tujuan v yang memiliki biaya paling sedikit saat ini.
- P(v): Ini mendefinisikan node sebelumnya (tetangga dari v) bersama dengan jalur biaya terendah saat ini dari sumber ke v.
- N: Ini adalah jumlah total node yang tersedia di jaringan.
Algoritma
- Inisialisasi
- N = {A} // A adalah simpul akar .
- untuk semua node v
- jika v berdekatan dengan A
- maka D(v) = c(A,v)
- else D(v) = infinity loop
- carilah w tidak di N sehingga D(w) adalah minimum.
- Tambahkan w ke N
- Perbarui D(v) untuk semua v yang berdekatan dengan w dan bukan di N:
- D(v) = min(D(v) , D(w) + c(w,v))
- Hingga semua node di N
Dalam algoritma di atas, langkah inisialisasi diikuti oleh loop. Berapa kali loop dieksekusi sama dengan jumlah total node yang tersedia di jaringan.
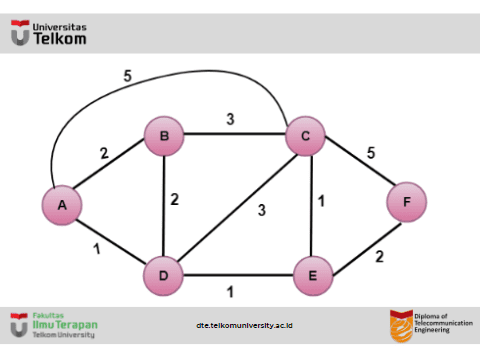
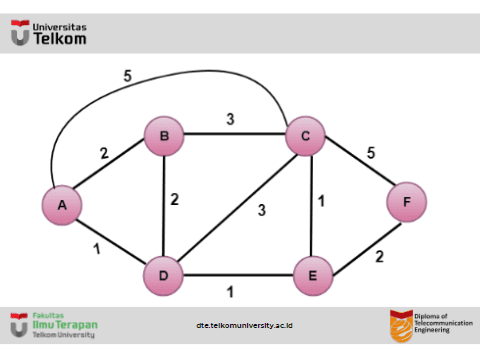
Mari kita pahami melalui contoh:
Pada gambar di atas, titik sumbernya adalah A.
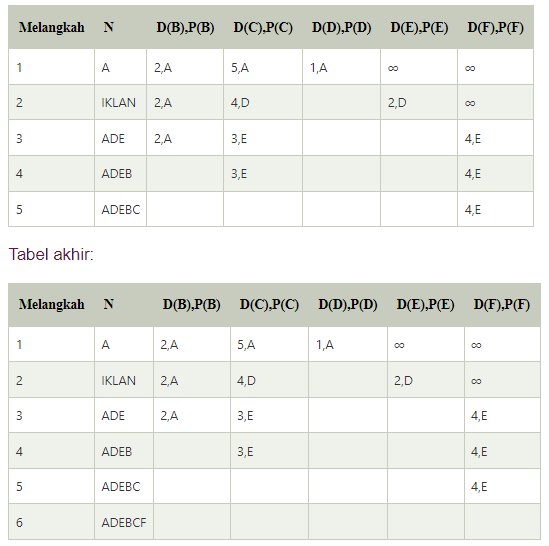
Langkah 1:
Langkah pertama adalah langkah inisialisasi. Jalur berbiaya terendah yang diketahui saat ini dari A ke tetangganya yang terhubung langsung, B, C, D masing-masing adalah 2,5,1. Biaya dari A ke B diatur ke 2, dari A ke D diatur ke 1 dan dari A ke C diatur ke 5. Biaya dari A ke E dan F diatur hingga tak terhingga karena tidak terhubung langsung ke A.
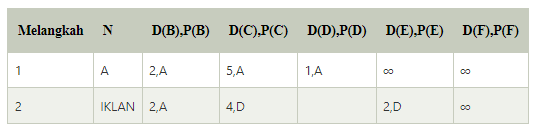
Langkah 2:
Pada tabel di atas, kita mengamati bahwa simpul D berisi jalur dengan biaya terkecil pada langkah 1. Oleh karena itu, ditambahkan pada N. Sekarang, kita perlu menentukan jalur dengan biaya terkecil melalui simpul D.
a) Menghitung jalur terpendek dari A ke B
- v = B, w = D
- D(B) = menit( D(B) , D(D) + c(D,B) )
- = menit( 2 , 1 + 2 )>
- = menit( 2 , 3 )
- Nilai minimumnya adalah 2 . Oleh karena itu, jalur terpendek saat ini dari A ke B adalah 2 .
b) Menghitung jalur terpendek dari A ke C
- v = C, w = D
- D(B) = menit( D(C) , D(D) + c(D,C) )
- = menit( 5 , 1 + 3 )
- = menit( 5 , 4 )
- Nilai minimumnya adalah 4 . Oleh karena itu, jalur terpendek saat ini dari A ke C adalah 4 .</p>
c) Menghitung jalur terpendek dari A ke E
- v = E, w = D
- D(B) = menit( D(E) , D(D) + c(D,E) )
- = menit( ∞, 1 + 1 )
- = menit(∞, 2 )
- Nilai minimumnya adalah 2 . Oleh karena itu, jalur terpendek saat ini dari A ke E adalah 2 .
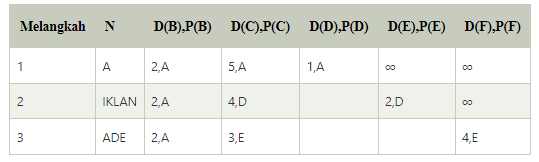
Langkah 3:
Pada tabel di atas, kita mengamati bahwa E dan B memiliki jalur biaya terkecil pada langkah 2. Mari kita perhatikan simpul E. Sekarang, kita menentukan jalur biaya terkecil dari simpul-simpul yang tersisa melalui E.
a) Menghitung jalur terpendek dari A ke B.
- v = B, w = E
- D(B) = menit( D(B) , D(E) + c(E,B) )
- = menit( 2 , 2 + ∞ )
- = menit( 2 , ∞)
- Nilai minimumnya adalah 2 . Oleh karena itu, jalur terpendek saat ini dari A ke B adalah 2 .
b) Menghitung jalur terpendek dari A ke C.
- v = C, w = E
- D(B) = menit( D(C) , D(E) + c(E,C) )
- = menit( 4 , 2 + 1 )
- = menit( 4 , 3 )
- Nilai minimumnya adalah 3 . Oleh karena itu, jalur terpendek saat ini dari A ke C adalah 3 .
c) Menghitung jalur terpendek dari A ke F.
- v = F, w = E
- D(B) = menit( D(F) , D(E) + c(E,F) )
- = menit( ∞ , 2 + 2 )
- = menit(∞ , 4 )
- Nilai minimumnya adalah 4 . Oleh karena itu, jalur terpendek saat ini dari A ke F adalah 4 .
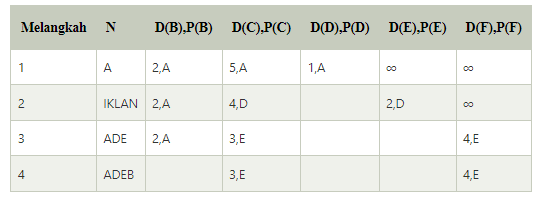
Langkah 4:
Pada tabel di atas, kita mengamati bahwa simpul B memiliki jalur dengan biaya terkecil pada langkah 3. Oleh karena itu, ditambahkan dalam N. Sekarang, kita menentukan jalur dengan biaya terkecil dari simpul-simpul yang tersisa melalui B.
a) Menghitung jalur terpendek dari A ke C.
- v = C, w = B
- D(B) = menit( D(C) , D(B) + c(B,C) )
- = menit( 3 , 2 + 3 )
- = menit( 3 , 5 )
- Nilai minimumnya adalah 3 . Oleh karena itu, jalur terpendek saat ini dari A ke C adalah 3 .
b) Menghitung jalur terpendek dari A ke F.
- v = F, w = B
- D(B) = menit( D(F) , D(B) + c(B,F) )
- = menit( 4 , ∞)
- = menit( 4 , ∞)
- Nilai minimumnya adalah 4 . Oleh karena itu, jalur terpendek saat ini dari A ke F adalah 4 .
Langkah 5:
Pada tabel di atas, kita mengamati bahwa simpul C memiliki jalur dengan biaya terkecil pada langkah 4. Oleh karena itu, ditambahkan dalam N. Sekarang, kita menentukan jalur dengan biaya terkecil dari simpul-simpul yang tersisa melalui C.
a) Menghitung jalur terpendek dari A ke F.
- v = F, w = C
- D(B) = menit( D(F) , D(C) + c(C,F) )
- = menit( 4 , 3 + 5 )
- = menit( 4 , 8 )
- Nilai minimumnya adalah 4 . Oleh karena itu, jalur terpendek saat ini dari A ke F adalah 4 .
Kerugian:
Lalu lintas padat terjadi pada perutean status Jalur karena Banjir. Banjir dapat menyebabkan perulangan tanpa batas, masalah ini dapat diselesaikan dengan menggunakan bidang Time-to-leave
AGR//
Referensi : [1]